M-ONLINE-INFO

Eine Scherung verändert nicht den Flächeninhalt

©1999 Richard Sachs

Im der folgenden Abbildung siehst du links ein Parallelogramm mit der Grundseite g und der Höhe h. Beachte, dass die Höhe h (immer!) senkrecht auf der Grundseite stehen muss.Schneidet man nun die linke Ecke (rotes Dreieck) ab und setzt es dann rechts wieder an die Figur, so erhält man ein Rechteck. Der Flächeninhalt dieses Rechtecks ist gleich dem des Parallelogramms. Da man beim Rechteck den Flächeninhalt als "Länge mal Breite" berechnet, ergibt sich nun die Formel für das Rechteck: A = g * h (* = Multiplikationszeichen). Diese Formel gilt dann auch für das Parallelogramm.

      Scherung

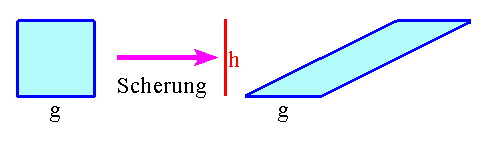
Man kann sich zum obigen Bild auch vorstellen, dass ein Rechteck durch seitliches Drücken zu einem Parallelogramm verformt wird. Diesen Vorgang nennt man Scherung. Wie wir oben gesehen haben, verändert sich der Flächeninhalt eines Vierecks durch eine Scherung nicht. Das gilt ganz allgemein. Betrachten wir ein zweites Beispiel:

Hier wird nun ein Quadrat durch seitliches Drücken zu einem Parallelogramm verschert. Das Parallelogramm hat aber immer noch denselben Flächeninhalt wie das Quadrat! Das wirkt zunächst etwas erstaunlich, doch folgende Betrachtung hilft: Bei der Scherung bleiben die Grundseite g und die Höhe h (im Bild unten roter Balken!) unverändert. Das sind aber genau die beiden Größen, die man zur Berechnung der Fläche benötigt. Wenn sich diese nicht verändern, dann verändert sich natürlich auch nicht die Fläche.